By the looks of the title, we'll be talking about a couple of seemingly incongruent topics today. Between the amazing three day weekend (which took us by surprise), the national holiday that may be the fifth fundamental force, and the recent detection of gravitational waves, there seems to be quite a bit that has transpired since we last published a post.
Let us start by apologizing for the delay. We are constantly trying to improve our website and as such have recently began reformatting some of the equations to make them a lot more user friendly and not reliant on third party sources. What this means for you, is more reliable service. But in addition to improvements that we have begun undertaking, we are also striving to revive our blog and start talking about issues that you care about. So if there's anything that you would like us to talk about, mention, or explain please feel free to either comment below or send us a line at info@TheEQNS.com
We would like to inform our visitors - from countries outside the United States or those who tend not to get involved in the current events - that this Sunday is Valentine's Day. A holiday mainly associated, and marketed, for love and companionship also brings mixed feelings for others who may not have a companion. For those of you fortunate enough to be in a relationship this Valentine's Day, strive to spend time with your partner. Spending time is far more important than spending money - it really is the thought that counts. So, if you're both into science and would like to do some problems together we will be here to help all weekend :D. For those who are single, don't fret. This is the PERFECT time to go out an meet a wonderful individual. The obvious eventual goal would be to use EQNS together of course, but we wouldn't blame you if you choose to wait until the second date to mention us.
On to more concrete issues. WE HAVE FINALLY OBSERVED GRAVITATIONAL WAVES. This is actually a huge relief because we have spend an enormous amount of money (over $1 billion) in our quest to find these waves. Let us take a step back and briefly talk about what gravitational waves are. Every force in nature has a corresponding quantum particle. Electromagnetic force for example has a corresponding photon. But recall that there's a wave-particle duality that exists. So while light can be thought of as a stream of photons constantly hitting your retina, they can also be thought of as waves. And much like waves, they propagate through space and cancel each other out. The same is true for the gravitational force. Instead of photons, however, the gravitational force is complemented with gravitons. Unfortunately, until just now, we had never detected a graviton. Gravitational waves are to gravitons what electromagnetic radiation is to photons. In other words, they're a different interpretation / representation of the same thing. For the purposes of this explanation, we're going to talk about gravitational waves as waves and not particles.
To detect a gravitational wave, scientists have to detect an expansion of space-time. Take a second to digest that statement. There are several questions that may arise as you are doing so. First, how does space-time change? Isn't it what makes up everything? Doesn't that mean that I took will be affected by it? And second, how does one go about detecting it? In response to the first questions, space-time is constantly changing. Anything that has gravity distorts space time. In fact that's the reason that objects orbit around each other. When you think of gravity from this perspective it no longer seems arbitrary. These gravitational waves essentially report a change in space-time. The larger the change, the more prominent the waves. The change that led to these waves being detected was a collision between two black holes over a billion light years away. If the distance doesn't shock you, the fact that we are only now detecting a collision that occurred a billion years ago may. Why are the two numbers the same? Because it took light a billion years to get to us!
So how do they detect these waves? Large structures are built to detect changes in length. Because gravitational waves both contract and expand space-time. If you send light going in one direction and get one number and send it going in another direction and get another number (for the length of two objects that were initially the same length) then you have just detected a gravitational wave! Unfortunately for this to work, the structures must be massive (miles long) and one has to factor out all of the noise. Additionally even trucks passing by can skew the results... So here's hoping that this isn't another neutrino-faster-than-light incident and that we have actually detected something that we once though was impossible to detect!
Here's to detecting more gravitational waves! Oh, and Happy Valentine's Day!!
Be sure to stay tuned to more blog posts and to check out some interesting physics equations on EQNS.
Also, don't forget to follow us on Facebook, Twitter, and Google+.
Let us start by apologizing for the delay. We are constantly trying to improve our website and as such have recently began reformatting some of the equations to make them a lot more user friendly and not reliant on third party sources. What this means for you, is more reliable service. But in addition to improvements that we have begun undertaking, we are also striving to revive our blog and start talking about issues that you care about. So if there's anything that you would like us to talk about, mention, or explain please feel free to either comment below or send us a line at info@TheEQNS.com
We would like to inform our visitors - from countries outside the United States or those who tend not to get involved in the current events - that this Sunday is Valentine's Day. A holiday mainly associated, and marketed, for love and companionship also brings mixed feelings for others who may not have a companion. For those of you fortunate enough to be in a relationship this Valentine's Day, strive to spend time with your partner. Spending time is far more important than spending money - it really is the thought that counts. So, if you're both into science and would like to do some problems together we will be here to help all weekend :D. For those who are single, don't fret. This is the PERFECT time to go out an meet a wonderful individual. The obvious eventual goal would be to use EQNS together of course, but we wouldn't blame you if you choose to wait until the second date to mention us.
On to more concrete issues. WE HAVE FINALLY OBSERVED GRAVITATIONAL WAVES. This is actually a huge relief because we have spend an enormous amount of money (over $1 billion) in our quest to find these waves. Let us take a step back and briefly talk about what gravitational waves are. Every force in nature has a corresponding quantum particle. Electromagnetic force for example has a corresponding photon. But recall that there's a wave-particle duality that exists. So while light can be thought of as a stream of photons constantly hitting your retina, they can also be thought of as waves. And much like waves, they propagate through space and cancel each other out. The same is true for the gravitational force. Instead of photons, however, the gravitational force is complemented with gravitons. Unfortunately, until just now, we had never detected a graviton. Gravitational waves are to gravitons what electromagnetic radiation is to photons. In other words, they're a different interpretation / representation of the same thing. For the purposes of this explanation, we're going to talk about gravitational waves as waves and not particles.
To detect a gravitational wave, scientists have to detect an expansion of space-time. Take a second to digest that statement. There are several questions that may arise as you are doing so. First, how does space-time change? Isn't it what makes up everything? Doesn't that mean that I took will be affected by it? And second, how does one go about detecting it? In response to the first questions, space-time is constantly changing. Anything that has gravity distorts space time. In fact that's the reason that objects orbit around each other. When you think of gravity from this perspective it no longer seems arbitrary. These gravitational waves essentially report a change in space-time. The larger the change, the more prominent the waves. The change that led to these waves being detected was a collision between two black holes over a billion light years away. If the distance doesn't shock you, the fact that we are only now detecting a collision that occurred a billion years ago may. Why are the two numbers the same? Because it took light a billion years to get to us!
So how do they detect these waves? Large structures are built to detect changes in length. Because gravitational waves both contract and expand space-time. If you send light going in one direction and get one number and send it going in another direction and get another number (for the length of two objects that were initially the same length) then you have just detected a gravitational wave! Unfortunately for this to work, the structures must be massive (miles long) and one has to factor out all of the noise. Additionally even trucks passing by can skew the results... So here's hoping that this isn't another neutrino-faster-than-light incident and that we have actually detected something that we once though was impossible to detect!
Here's to detecting more gravitational waves! Oh, and Happy Valentine's Day!!
Be sure to stay tuned to more blog posts and to check out some interesting physics equations on EQNS.
Also, don't forget to follow us on Facebook, Twitter, and Google+.

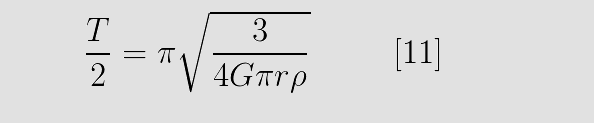
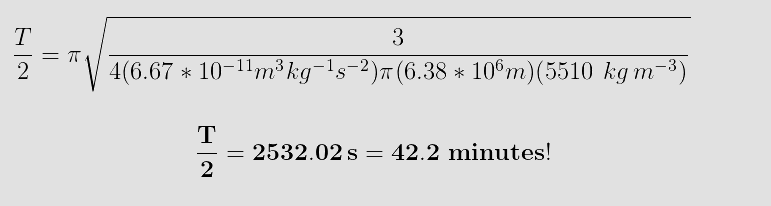












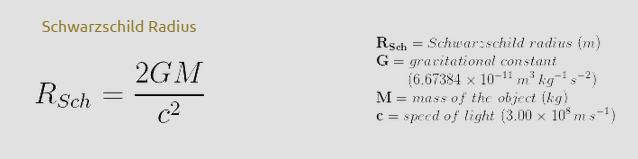

 RSS Feed
RSS Feed